What the Hell Does Statistically Significant Mean?

There are three kinds of lies according to Mark Twain, "Lies, damned lies and statistics". There was even a book called How to lie with statistics. Whats so important about statistics and why would people call it lying? Its a two pronged question that ill try to fully explain. Believe me even I get a bit confused when trying to explain statistics.

Huh!?!

First statistics is the backbone of modern scientific work. Because of the complexity involved in modern research and the importance of major breakthroughs we need to collect tons of data. Modern experiments simply aren't aiming at low hanging scientific fruit anymore and potential gains may be almost minimal or indistinguishable from background noise. So, we collect data, lots and lots of data. On any study there may be thousands or even millions of data points to sort through and process and statistics is how we do that. 

The assumption of statistics is that if there was an absolute value to something that you could measure, you would never measure that exact value every time no matter how accurate your instrument. Assuming you had an infinite number of measurements even though they weren't all the same, the average or mean of the sample should represent the true value. Clearly an infinite number of measurements is impractical for reasons of both time and money so we use statistics to give us an idea of what that mean could be with the data we can gather. Think of it kind of like a plinko distribution.

Statistics: making game shows boring since forever

Any one of those balls could end up in any one of those slots when dropped but the overwhelming majority will end up in the middle. So how do we use that in science? There are essentially two ways that statistics gets heavily used. 

The first is to essentially try to find a connection between an observed result and a bunch of possible variables. We're essentially looking for a correlation between variables. So for instance I have two cats and Id like to test to see how I can make them more cuddly (wicked gay experiment I know bear with me). So I'm attempting to figure out what triggers the desired behavior from the following variables: how much food they eat, the sugar content of the food, how much sleep they get, how recently they took a bath and positive reinforcement. At the conclusion of my experiment I can test each variable for a relationship to my target behavior (cuddles). If I find a relationship between baths and positive reinforcement but no others I can rule out food sugar and sleep. Now assuming this relationship is positive on both accounts that doesn't mean that continuous baths or treats will always yield more cuddles, it means that further testing is required under more controlled circumstances.  

If you said aha you were limited in what potential options could affect the outcome congrats gold star to you. If you said ahaha that proves crap, their may be influences like free will that essentially nullifies the experiment except in the broadest sense you get a 1 UP mushroom because your awesome.  

Yay Video games

What you just stumbled upon is the golden rule of statistics and also the most frequently ignored. CORRELATION DOES NOT AND WILL NOT EVER PROVE CAUSATION. The closest you can get is a single variable system like say pushing a toy car AND you can link the effect to the cause with a mathematical relation. See the second rule surrounding correlations is they can only be found using straight lines.Those lines can be mathematically rearranged to be straight but at the end of the day they have to be straight and they have to be lines. If you don't follow those rules bias is likely to creep in and you can find whatever you want to see.  So when you see people linking 

To This

Its kind of, sort of shoddy statistics. See the lines both go up and they both seem to be on an exponential ish curve but there is a hell of a lot more variability in one than the other. That's not to say that they cant be linked or shouldn't be linked but that temperature data needs to be cleaned up a lot. That's right folks it's a climate change article huzzah. Which brings us to the second major use of statistics in science, prediction.

See once we have our theories we need to test those theories, this is science after all not psychology (that link remains until Carol Gilligans crackpot theories with no evidence are cast out from textbooks, I can hold a grudge quite well Westfield (-.-)). So once we have a working model; one that cleans up all the data and variables to show the trends as clearly correlated; we need to test that hypothesis and model. In the case of climate change that is done by both back casting climate, and attempting to forecast it.  But how do we know if were right and not just making some crap up. Well prepare for a fun lesson in statistics.

Normal Distribution

Above you see whats called a normal distribution curve. It's not really useful as it technically doesn't exist (outside of math and theory), but it is the base of all statistics, gaze upon it.  The numbers on the bottom of  the curve represent whats called a standard deviation. Each standard deviation away from the midpoint/zero/base point contains more of the data as a direct percentage of a theoretical infinite sample size. You can see those percentages within the brackets, so within half of a standard deviation 38.2 percent of the total data is contained, 19.1% on both the left and the right. 

You may have heard of the 95% confidence interval or statistical significance (hint: its what this terribly boring thing is about). While arbitrary, it essentially means that 95% of my collected data should fit within about 1.66 standard deviations from the mean. So when testing a theory the mean is my hypothesized value and the standard deviation is my error typically reported as a +/- value or percentage of the hypothesis. There is actual math to determine your standard deviation it is not a guess value and cannot be arbitrarily changed because your data doesn't line up. When determining significance, what we are essentially saying is the probability of the data matching our mean by chance is 5% or less.

So lets put all of this together for hypothesis testing. Let's say I made the claim that I was like a human thermometer. Not only could I tell your temperature, I could do so merely by looking at you and my accuracy would be within +/- .1 degrees Fahrenheit. It's an awesome claim so we design an experiment, we take 1000 volunteers who I simply look at through a photograph. The temperature of all participants is taken at the same time of the photographs. So I proclaim every single photograph has a temperature of 98.6 degrees (this is the natural average anyways). Now lets say the actual data lies within +/- 1 degree rather than the +/- .1 degrees I claim. My proclaimed accuracy is essentially falsified.  Even if the mean of all those temperatures is 98.6, and the accuracy is correct, it still doesn't prove my claim that I can accurately tell human temperature from appearance. This is a demonstration of correlation vs. causation error.

Artists depiction of me reading temperature

So how do we apply this to climate change? Well lets assume that I have a model projection of what the global average temperature should be (my mean) and because I'm super smart I did all the very painful (it truly is excruciating) math to determine my error (the standard deviation). In order for me to be correct about both my mean and standard deviation, 95% of the sample data should fit within 1.66 times my standard error from the mean. If the data is scattered so as not to be significant either the hypothesis, the margin of error or both are incorrect. That's assuming the data is scattered outside of both tails of the curve. If however the data is scattered only outside of one tail (like being below all estimates) then we can say that the probability of the hypothesized mean being correct is less than 2.5%.  So the probability that climate change/global warming/extreme weather forecast predictions and models accurately depict the future is less than 2.5%. Think about that for a moment.

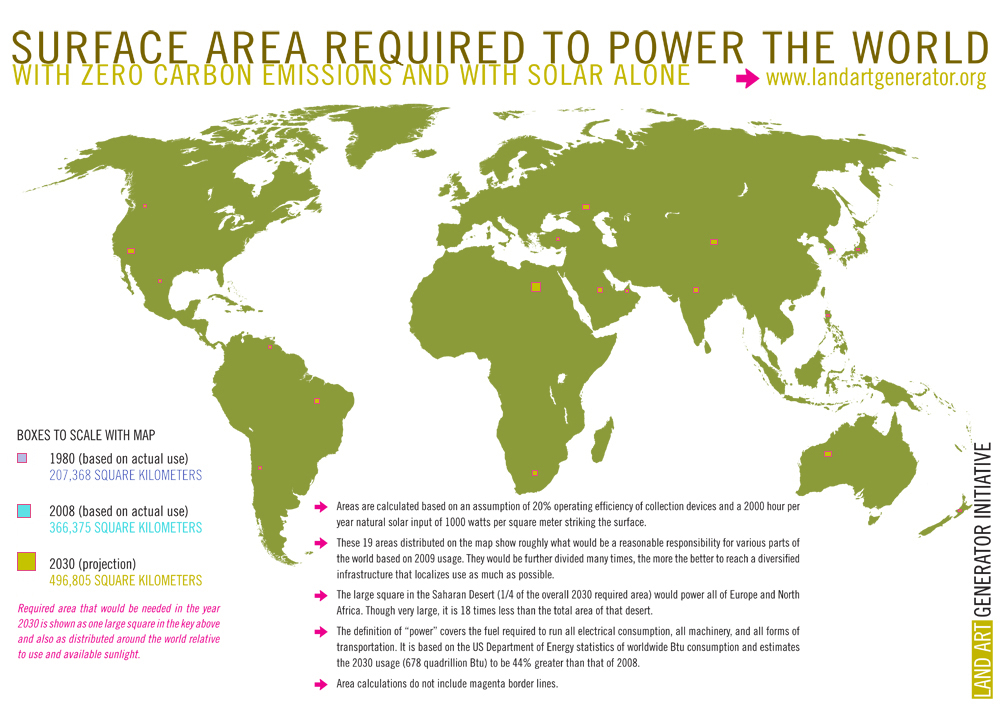
Out of 34 models when the estimates are averaged together (a reasonable practice with a multiple estimate scenario) actual temperature is below the predicted temperature below the level of significance and has been for almost 18 years. Now almost all of these models don't find significance on their own, only a few actually show some significance with actual data. So in short the probability that the settled science, that the claims for trillions of dollars in alternative energy are neccessary to avoid catastrophe, have a less than 2.5% chance of being correct. I have mentioned the precautionary principle but frankly that's just absurd.

So how do climatologists plan on handling observational discrepancies? Well I know I have faced this challenge with computer models that I designed and my response was to start from scratch; I'm also fairly rigid in how math and science should be applied. One potential solution to the discrepancy is to expand the margins of error for the estimates. An interesting choice considering the largest criticism of climatologists is that they are overstating their confidence and position. The other is to wait for more data.

These choices bring about other issues aside from the due chiding in the public arena; and proof that the science isn't as settled as is claimed). They can only expand those uncertainties so much before the models predict cooling, warming and no temperature change at all.

If' your theory is proven correct by all potential outcomes it is not falsifiable. If a theory is not falsifiable than it is no better than a religion. 

Whats So Scary About Nuclear Power?

Warning Diehard movie spoilers ahead:

I watched Diehard last weekend and it was entertaining; huzzah explosions and all that. I only had one issue with the movie and that was the complete misunderstanding of nuclear energy. My instinctual anger at horrible physics was related to one scene in the movie, it wasn't even 30 seconds long, yet there was still soo much misinformation.

The plot of the die hard movie revolved the idea that Chernobyl was a man made accident (it was) which was brought about by illegal weapons merchants getting greedy selling reactor byproducts or fuels (it wasn't). There was a warehouse containing weapons grade uranium 235 which, would simply not happen as a reactor byproduct or a fuel, and even this didn't set off my bad science alert. I'm more than willing to accept some fudging of accuracy for the merits of storytelling. I got pissed off when they entered the warehouse containing said uranium and determined the radiation had been pooling for decades, and they had a spray to neutralize it. Those two statements actually angered me.

Nuclear fuels and waste products are relatively safe. You don't want to put them in your pillow and sleep on them every night but handling them is not some sort of life threatening risk. Diehard even accurately depicted this, however they had to clean up "pooled" radiation. Radiation isn't a gas or a liquid. It simply can't, ever or under any circumstances pool. Radio-nuclides don't become more dangerous over time. Radiation radiates, until it hits something and is absorbed.

Yep not really great against radiation

 It's pretty simple, and yet someone felt they needed to address this issue write a script, develop a technology and CGI the cleaning of the radiation for something that simply wasn't even a major plot point.  They even said the fuel is stable and there are no major short term exposure risks. They took off their protective suits. Maybe I'm perseverating, but to me, Hollywood acts like it's some sort of intellectual mecca, yet no one on a big budget movie said hey this is dumb. The fact that they filmed the clip, which again wasn't a critical plot point at all, and then dumped it on the public is more indicative of a fundamental misunderstanding of nuclear physics in the general populace.

From the above image you can see the four main types of nuclear radiation and the corresponding materials required to stop them.

Alpha Radiation: Alpha radiation is the same thing as a helium nucleus its large and that's why it can be stopped by paper. Not really a threat to anyone.

Neutron Radiation: Neutron radiation is essentially only produced during a nuclear reaction, its barrier requirements are very high and it essentially disappears when a reactor is shut down.

Beta Radiation: Beta radiation comes in two forms beta + and beta-. This is simply an electron or the oppositely charged component called a positron. It is readily stopped by stuff that's thicker than a piece of paper and beta emitting material is usually trapped in the pipes circulating around a reactor.

Gamma radiation: Gamma radiation is essentially light, its light that we can't see but its just light. It's emitted from particles and in the reactor. overwhelmingly gamma radiation is what people are referring to as radiation in a nuclear plant.

From this synopsis you should be able to get that the only two types of radiation we worry about is beta and gamma, the others only exist when the reactor is running or are essentially nonthreatening. Beta emitters are produced as some of the fuel degrades or byproducts escape into the water. In a nuclear plant beta radiation is safely contained in pipes. The only time it becomes a threat is when work has to be completed, assuming proper procedures are followed (they are or you get fired) the exposure and risk is minimal. The only radiation truly worth tracking is gamma exposure.

Both beta and gamma radiation are produced from radio-nuclides breaking down into more stable component's. nuclides that break down are called radioactive. If you just said aha that's why radiation levels couldn't have been worse after fifty years you get a gold star. As more of a nuclide breaks down there is less remaining, so radiation levels drop. The way we measure the activity of decomposing material is through half lives. A half life simply put is the period of time required for you to have half of the starting radioactive material.

Uranium is all natural so it must be safe :-P

So how dangerous is the material, well that depends on the half life and the amount of time elapsed. Because Uranium 235 has a half life of about 703 million years its not all that dangerous. The statement "A candle that burns twice as bright burns half as long" is a solid analogy. Radio-nuclides that have really short half lives are dangerous but not for a very long time. There are some radioactive materials which decay into more radioactive materials before becoming stable but these are uncommon.

So what makes an element radioactive? Well in short it's the number of neutrons an element has (protons and electrons define what the element is).  The total number of protons and neutrons determines the atomic mass of an element. The different atomic masses are what we call isotopes which is is the difference when talking about Uranium 235 vs. say the more common Uranium 238.  The difference between these two isotopes is 3 neutrons and that difference makes uranium 235 more prone to undergo fission in a nuclear reaction. We can say that Uranium 235 is more fissile than Uranium 238.

Nuclear  Energy: think of the amount of nuclear energy derived being equal to the difference between your staring element and final element

So how do we get Uranium 235, well hydrogen and other elements undergo fusion in stars but that essentially only forms iron. When stars supernova the released energy forces fusion to higher elements.  Then as time goes on the unstable elements decay leaving the more stable ones behind. Uranium 235 may have the impressive half life of 703.8 million years but Uranium 238 has a half life of almost 4.5 billion.  This leaves us with a relative abundance of about .72% Uranium 235.

We like Uranium 235 though, its easier to use so we have to .... enrich the uranium sample. How do you do that? Primarily through diffusion. In short because Uranium 235 is less massive than Uranium 238 it moves faster. So if you turn the uranium into a gas or a liquid through chemical processes then attach this to a really really long tube or series of tubes the Uranium 235 and Uranium 238 will flow at different rates. Considering were talking about a 3 neutron difference this process is needless to say fairly expensive.

Lot's of tubes and a really long time

The higher the purity you need the more expensive, and difficult it is to produce. That's why I said enriched Uranium not weapons grade. See nuclear reactors don't run on weapons grade, they don't even run close to it. Most reactors run on less than 5% Uranium 235. In fact most reactors aren't too picky in terms of how well refined the fuel is. A few reactors particularly molten salt reactors need less than 2% Uranium. There are a few reactors which run with higher enrichment such as research reactors and military nuclear reactors but they are the exception rather than the rule. The rest of the fuel is a ceramic material coupled with  a few other fissile materials. For a comparison weapons grade uranium hovers around 80% Uranium 235.

How do we know the limitations and that rectors wont go boom? Well that has to do with the measurable concept of criticality.  Criticality is a fancy way of saying whether a nuclear reaction is slowing, speeding up or maintaining speed.  The definition of criticality is essentially dividing the current generation of free neutrons by the previous generation. if the value is 1 the reactor is running critical, if the value is greater than 1 the reactor is running super-critical and if the value is less than one it is running sub-critical. Yes reactors run critical or super-critical all the time and no one dies (unlike the movies). When the control rods are withdrawn from the fuel cells the reactor will run super-critical until it becomes critical.

So when we are looking to blow crap up we know that we need the number or unrestricted neutrons to essentially remain critical while the rest of the material explodes. the less refined the material the more of it is needed to maintain this unrestricted fission.The mass of material needed to maintain the number of neutrons generated is known as the... critical mass. At a 6% concentration of Uranium 235 the mass required to sustain a nuclear blast is infinite. This doesn't just mean that reactors won't go boom, it means they physically can not.

It also means the Diehard explanation for Chernobyl is a bit flaky, if the bad guy was buying weapons grade uranium to run as fuel then the operators would have simply adjusted the reactor to run critical, no boom. If he was trying to run the reactor to produce Uranium 235... well he cant.  The original concerns were for reactors producing plutonium which would still require enrichment to be weapons usable. This would have again collapsed the entire story. Like I said it was a story telling device so I tried to merely grimace. It would also mean that in order for the plot to have happened socialist governments have to be the most corrupt bribe taking ...oh wait never mind.

So what did happen at Chernobyl, or Fukushima? and what is a meltdown? Nuclear plants and reactors are inherently safe. In fact you either have to try to cause them to fail or there needs to be an act of god. This actually explains both Chernobyl and Fukushima but only vaguely.  The only weakness to a nuclear reactor is its coolant supply. See nuclear reactions release a lot of energy, literally shit loads of it. Even with the control rods in there is still some latent heat and reactions occurring. As such cooling water must always be supplied to the reactor even during shut down. Even the spent fuel has a cooling system. A lack of cooling over a prolonged period of time will start to raise temperatures significantly. If things get too hot parts fail.

See Chernobyl was a byproduct of Russian engineering which is an oxymoron like military intelligence. It was also a generation 1 reactor built as a publicity stunt by the soviet empire. In short it was almost doomed to fail.  Chernobyl had no form of containment, there was no cement dome or pressure seals or really any safeguards in case of equipment failure.  But even that oversight wasn't as dumb as the reactor operators deciding to run a drill around coolant failure procedures... by actually shutting down the coolant.  Im guessing USSR school fire drills must have consisted of lighting the school on fire.

By the time they decided to restore cooling the plant had failed, the components had gotten hot enough to start producing flammable gasses. This exploded breaching their lack of containment with a variety of radioactive salts and byproducts. So that's kind of a bad problem, whats worse is it happened behind the iron curtain and information and aid was refused by the soviets. All in all the total death count was.. 31 people. That's it the largest nuclear disaster in the history of mankind killed 31 people. There are other estimates which are higher but 31 is the only actual number of solidly recorded deaths.

The next big nuclear disaster is Fukushima, which resulted after a massive earthquake and tsunami basically destroyed all power and utilities transmission to the plant. As a result of not being able to maintain pumping capabilities the reactor overheated and ... oh ya there was containment.  Only one of the reactors breached containment.  and the release was not all that bad. 0 people died in the incident. Most incident reports and even a lawsuit are alleging that the government and a lack of a questioning attitude are to blame for Fukushima. Fukushima was another publicity nuclear powerplant, attempting to show the world the glory of Japan.

So what does that mean for us? Well we learned a lot from these two disasters. modern plants are being designed with automatic redundancies and gravity based cooling systems. Because of current design modification plants are able to be produced almost 80% cheaper than in previous years even with extra redundancy systems. The Westinghouse AP1000 is so well designed that we are actually seeing nuclear plants constructed again after a halt in production for almost 30 years in the US. Like I said nuclear plants are insanely safe and they generate crap load of power. Nuclear power is the safest source in terms of deaths per trillion kilowatt hours with 90, wind comes in second with 150. Its also got the smallest carbon footprint for those who care.

I have explained how radiation works, and how it's not dangerous. I also explained how nuclear plants are inherently safe and how some of the terminology should be applied to them.  What I haven't covered is where the energy comes from. That's important because its the easiest way to explain why nuclear power will always beat out wind and solar. We started walking down the nuclear road after Einstein's famous equation E=MC^2. For those who don't read math it states that  the energy that can be produced from a given mass is the same as that mass multiplied by the square of the speed of light.  The speed of light is a big number so squaring that means that only  a little bit of mass is needed to make that change. you can find estimates around to try to get an idea of how much energy is in uranium but a pound of uranium contains as much energy as about 3 million tons of coal.

I'd rather not show the math for a fission reaction because fusion is simply easier and demonstrates the same principle. First lets look at a hydrogen from a periodic table.

Ok I lied that's deuterium an isotope of hydrogen containing an additional neutron. You can do the same thing with hydrogen but the result is a lot less stable and the math is more complex. So now were gonna grab some helium.

Were going to use  2 kilogram moles of deuterium to produce 1 kilogram mole of Helium. a kilogram weighs about 2.5 pounds so this is about 5 pounds of stuff. A mole basically is the atomic mass of something in the units I want to measure. It ensure a relatively consistent number of atoms for the reaction so I'm starting with 4.028 kg of deuterium and through fusion producing 4.002602 kg of Helium. so the math is 4.028 kg-4.002602 kg=.025398 kilograms of mass lost. not a whole hell of a lot of mass lost but all of it and I mean every bit of it is converted to energy. So pulling out Einsteins formula .025398*8.98755179*10^16 m^2/s^2, or 2.28*10^15 watts.

That's a shitload of energy but really doesn't mean jack to me. That's a number bigger than my comprehension so how long would that amount of energy power a 100 watt light bulb. so we take our value divide it by 100W*24 hours/day* 365days/yr.
(.025398*c^2)/(100*24*365)=2.6*10^9 years so our 5 pounds of stuff is capable of powering a lightbulb for 2.6 billion years. Granted the max efficiency is gonna be somewhere around say 40% so that 5 pounds of stuff will realistically only power that light bulb for around a billion years.  Lets leave it at a shitload of energy.

Of course that's fusion but fission reactor potential energy isn't that much different even if it was off by a factor of 100 its still crap loads of energy. That energy abundance is why we don't realistically have to worry about running out of energy and why we have plenty of time to figure out fusion. Uranium isnt the only fissile element, while its currently used in modern reactors there are other technologies available.

Currently research is resuming on molten salt and thorium reactors as the generation 4 technology. These reactor types were abandoned due to political pressure but they are actually safer and more abundant than current uranium reactors (fun fact uranium is more abundant than silver). Assuming a switch to these technologies it would mean that meltdowns would be even less likely to occur if not impossible.

Fun fact modern nuclear power costs are around 6-7cents per kilowatt hour coal and natural gas is about 3-5cents and wind and solar run around 12-20cents per kilowatt hour depending on the technology. with gen IV reactors looking to be cost comparable to coal i think we can kiss wind and solar goodbye..... without political intervention.

Why Liberals Are Anti-Science part Douche (2): The Precautionary Principle

The reason I started this blog is that I have a crap load of knowledge on science, research and the like. The lack of understanding among the general populace is actually kind of irritating to me, rather than sit in a corner and moan about the world I'm going to do what I can to correct some of the misinformation or misunderstanding that's out there. Every once in a while I'll venture into politics, I'm not perfect, but the reality is I'm a scientist to my core. I know I don't reach a lot of people with this blog and I'm too stubborn to develop a larger network for greater visibility. If you like this article or agree with it repost it, because what follows is a discussion that should be thrown around whenever anyone starts saying conservatives are anti science.

Like I said before both republicans and democrats are "anti-science". The difference to me between liberals and conservatives is that conservative "anti-science" beliefs are essentially harmless.  Who gives a crap if some voter doesn't believe in the theory of everything or evolution. They might be idiots but they honestly aren't harming anyone but themselves.I think the only conservative position I have taken issue with is stem cell research and that's a question of ethics. If i was paralyzed and someone told me a fetus could let me walk again I'd head on down to the local abortion clinic with a blender in hand.  I clearly cant speak for everyone and i know that.

The thing about liberal "Anti-science" beliefs is that they are numerous. The crusades are against well established technologies and they cause people to die.  I'm not exaggerating, in addition to clear ignorance on climate change data there are lefty groups against all of the following technologies, each one is worthy of an article: Nuclear Power, Genetically Modified Organisms, Vaccines, Modern Farming Techniques, DDT, Electromagnetic Waves, Natural Gas and Fracking Technologies, Animal Husbandry,  Aqua Culture, Psychotherapy,  Cooked Food, Affordable Power technologies, and Oil Production. I mean I could go on, but really, do I need to? There are literally so many scientific technologies that liberals are against that I get to have a great laugh when they start protesting against one another. There was even a paper I saw in the past year of liberal groups promoting the idea that we should make food more expensive through legal regulation.

Silliness aside, and back on the issue of liberals killing people. What upsets me about this is the stance from those defending team blue. Ideas like 'it's not antiscience if you know and understand the principles of the theory and technology' isnt a defense to my challeng.  In my mind you are literally saying you understand that hunger,  disease and poverty can be cured or at the very least alleviated by these technologies but you would rather spend the time, effort, and energy protesting them. If you agree with that statement then you are literally saying that you sanction the deaths of millions of people on an ideological wet dream.

The reason for the slaughter is called the precautionary principle. At its core the precautionary principle goes like this, its OK to oppose something, because we don't know what the effects are gonna be down the line.  Sounds somewhat reasonable right? I mean you wouldn't want to do things to harm yourself or your children.

The problem is with all of those technologies I listed above, with climate change, Is that we really and truly do know. Much of the protested technology has been around for 50 years or more and liberal still actively form legal hurdles. All of them have been proven safe not just with actual practice but with tons of research. Even if it wasn't, which it is, just because you don't know whats going to happen 20 or 30 years or 60 years from now doesn't mean a chain of  events leading to disaster is likely or probable.

Do you know that guy? His name is Norman Borlaug and he won the Nobel prize for vastly improving crop yields through both new farming techniques and genetically engineering better strains of plants. He is kind of a big deal because he helped make crops grow in regions where they normally don't. See that at the core is what genetically modified organisms are for, we take useful characteristics and share them, even cross species which would be otherwise impossible. It's the same stupid thing that human beings have been doing with selective breeding, except its faster, more accurate and easily replicable. Sure we might make glow in the dark rabbits and monkeys but that's just for shits and giggles, and oh by the way I have actually done genetic engineering to make that glowing protein. No Tesla coils or other mad scientist stuff.

Yes its super creepy

So why would people protest better crop yields. Well for one there's always fear of contamination after all bees don't exactly stop at fences. But who would get mad at better crop yields? Monsanto has patent lawsuits over them sometimes but that's no reason to protest GMO's entirely. Of course there are risks like creating more resilient pests, but that doesnt stop us from producing or providing antibiotics, and even so why would you protest draught resistant crops? Well its that damn precautionary principle again. I mean what if something bad happens at some point due to the dna your eating today or what if it genetically modifies you?

Well folks your in for a treat, here's what happens when you eat something. First you cook it which essentially destroys or denatures most if not all of the proteins. It is then chewed, producing more surface area for the acids and enzymes in saliva to break down all those proteins. Then it hits the stomach acid which breaks it down even more. Almost to the point of containing no proteins at all. This slurry of amino acids (protein base components) then enters your intestines where more enzymes are secreted, basically destroying any remaining proteins. whatever sugars in that soup and amino acids are absorbed. What few proteins have survived your bodies best attempt to destroy them don't, because they are too damn big to pass through the membranes. So bacteria eat them and break them down further into other components which we can use.

In short what you eat is broken down to its fundamental components so that your body can make it into whatever thing it needs. See why would you have evolved over billions of years only to have to use the proteins that your food had. Do you have any idea how much and how varied our diet would have to be to survive that kind of requirement? It's ridiculous, by the time your body gets to use the tomato you ate it is no longer even remotely recognizable as a damn tomato GMO or not.

Do you know that guy? Well you should he's Louis Pasteur and kind of sort of the father of the modern vaccine as well as a whole slew of other amazing experiments. He is to microbiology what Galileo is to physics. What I'm trying to say here is vaccines are old, really old, like hundreds of years old.  You see he wasn't even the first person to consider inoculation. The concept of using an inert virus or bacteria to stop you from dying of well something super nasty may be as old as 3500 years. Vaccines are so effective that we have wiped some plagues from the face of the earth. They are so useful that you probably didn't have a friend stuck in an iron lung.  Who the hell would protest anything that is cheap and effective at stopping the nastiest of diseases?

Well the short answer is idiots.  I don't use that term lightly. See protestation of vaccines comes from some horribly misguided belief that the vaccine causes autism. As to why, well there was this study, which violated every scientific principle known to man, and was still published. It has since been retracted and no one I REPEAT NO ONE HAS EVER BEEN ABLE TO VERIFY, OR EVEN COME CLOSE TO A LINK BETWEEN THE TWO. There was also mercury in some of the earlier vaccines (hint: its actually a great preservative) which was in such small amounts as to be nonthreatening.  If you want to argue about that point I dare you to go read up on dosages and find me a scientific article showing it as a problem.

So now we have a situation where a bunch of idiots have actually caused outbreaks of diseases that we once had effectively bottled. Not just here in the US with outbreaks of whooping cough but in overseas countries. there is effort to delay or stop implementation in the third world through widespread fear campaigns. If you know someone in this movement and they truly know that all of the research says otherwise than punch them for me. I mean seriously give them a solid whack in the face, and if they didn't vaccinate their kid, infect them with polio. Its the best way to make a point.

This doesn't even touch on DDT. DDT is one of the safest, cheapest and most effective mosquito controls ever invented. Its one of the best ways to prevent malaria. It was banned in the US and many developing countries because it might have caused problems with bird populations. To be clear before DDT was invented bird populations were on the decline, and they recovered before dispersal was ever stopped. But even if it was a problem for birds, what is the loss of a few birds to save literally millions of people each year.

Do you want to know why so many Americans have a smartphone? Ill give you a hint it wasn't the greenies. What really helped America grow wealthy and prosperous was industry. The ability to process raw materials into useful goods.  I know it sounds crazy but that's why we burned fossil fuels. So logically if we want to help the third world out of poverty clearly the best approach is to let them industrialize. While coal and oil may not be the best sources of power they are the cheapest. Not in terms of fuel costs but in terms of capital costs. That means that more power can reach more people with coal oil and natural gas than wind, solar or even nuclear.

I said I oppose liberal groups because people die from their actions. I oppose them because they literally want to make life harder on people. Rather than pooling their money and resources to put up the projects they support they spend that capital trying to take other people down or buying votes. They use fear and misinformation to spread unscientific discourse, because frankly, fear works. They stand in the way when people attempt to build what they need. Does anyone really think that the Canadian oil sands aren't going to be developed if there is no keystone? The choices aren't to stop the project and help the planet vs jobs, its American jobs vs Chinese jobs. In the developing world its science and technology vs. death.

In the US we are rich relatively speaking, we can afford the luxury of medical care and exorbitant food pricing. That doesn't means its even remotely right to try to sell luxury ideas to starving nations. If we were to implement organic farming techniques over existing land we would only be able to feed about 4 billion people. With almost seven billion people in the world, if liberals know the scientific facts, it would be pleasant if they simply volunteered to die first.

Q:What do Christopher Dorner and Drone Executions have in common, A: Gun Control

Power creep is inevitable.  You see it all the time in gaming, in DnD every new book contained powers or abilities which surpassed those of previous books. In World of Warcraft, or really any MMO you see new abilities and gear that makes you more powerful tier for tier than previous versions.  All games give us new things, its what keeps us glued to our monitors or TV's. The thing about gaming power creep is that if they introduce something new that we don't like or that grossly unbalances the game, we can leave. That's not so true for government.

See government also experiences power creep. every generation of lawmakers or presidents wants to surpass the previous generations. It's not necessarily malicious. This happens at all levels of the government. Reason.com recently had a post detailing a list of events and occurrences of police mischief where citizens died due to police misconduct or zealotry  and that was only in the past few years. In most of these cases there is a marked lack of responsibility and the perpetrators are rarely, if ever, punished. If you want a more visual example there's this map from the Cato Institute detailing botched swat raids. The Cato Institute also released this map of police misconduct and that's just from 2009 and 2010 incidences.  I'm sure you or someone you know has their own story.

While my encounters with police aren't as rapey or murder prone, and i'm not some sort of legal or ethical saint, I have still faced questionable ethics and law enforcement.  I have been pulled over and yelled at by an officer who followed me for over 2 miles with his lights off hoping he'd get a DUI bust out of it. I have been pulled over for traveling in the left hand lane of the mass pike. One of the funnier incidents was when I received a written warning that my inspection sticker was going to expire in a month. The most powerful incident was the summons I got for minor with transportation when I was a designated driver, that one drove me towards my libertarian outlook. But my favorite abuse of power is this ticket that my signiicant other Robyn received over the summer.

Looks like any other ticket but there are a few fun discrepancies. First it says that we were traveling 72 in a 40 on interstate 93, the problem... There is no 40 mile an hour zone. The lowest speed limit is 45mph which wasn't even where we were stopped. why on earth would an officer lie about such things? Well the difference between 72 in a 40 and 72 in a 45 is about 185$. see your charged 5$ per mph over the speed limit and that goes up to 10$ per mph for speeds greater than 30 mph.  There are a few other details in the ticket that irk me and show either massive incompetence or a lack of sobriety on the officers part.

But why shouldn't an officer lie. I mean their paid not to, but their also paid to serve and protect not shoot your dog on your property without a warrant. All an officer has to do is say he didn't do something and fellow cops, DA's, the courts, and unions will stand in the way to protect them regardless of the charges or evidence. prosecution is just starting to occur due to the widespread use of cellphone cameras, thank god for technology.

Which brings us to Christopher Dorner. He alleged that a partner of his kicked a  mentally disabled man, a charge which the man and the mans father corroborate. He was then fired when the offending officer was cleared. I dont pretend to know what really happened that day. I do know on the appeal of his termination a judge declared that there was evidence that he wasn't lying, I also know the case is being reviewed again, and that the LAPD is notoriously corrupt and abusive.

Without a trial Dorner met his end when the police decided to light his cabin on fire using gasoline.  They of course deny trying to light the cabin on fire but there is a video so take that as you will. I don't condone his acts of violence but we need to be consciously aware that the LAPD decided without a trial or a jury to execute a man for his crimes. Is that really a power we want a notoriously corrupt group to have?

 What about the shots fired into a civilian pickup that simply looked like Dorners' shouldn't we at least punish them for that.

Pictured: Police Prudence

The drone strikes against Anwar a-alwaki and his son raise the exact same questions for president Obama.  In this case we have the execution of an american and his son without trial and jury, that's bad, that's incredibly bad, in fact the history of the modern legal system and governance is based entirely around the prevention of such unilateral power. Being judge jury and executioner isn't the only legal liberty Obama has taken, there's indefinite detention, the undeclared wars, bypassing congress for appointments and many many other civil liberties and legal violations that the executive branch has taken. Are these really the powers we want the government to have over us? Even if Anwar al-alwaki committed terrorist acts, which there is no evidence he did, doesn't he still deserve a trial? Isn't that in the constitution

It used to be that there was ample opposition to such power grabs and brutality. The antiwar movement, democrats and liberal media criticized the abuses of executive power. That was until their man got elected of course. Obama is defended by these has been critics of Bush. The government is ripe with hypocrisy. Apparently injustices are only unjust when its not your man pulling the trigger. This acceptance or silence in the face of federal power seizures is why we experience power creep.

In the gun control debate there were some choice bits from gun control advocates. Anything from how the second amendment protects muskets to how its about sport shooting.  The reality, and the somewhat discomforting fact is the founding fathers were well aware of power creep. The bill of rights is what is supposed to stand in its way, assuming a strict interpretation.  That's why there is some very frank and clear language in there such as congress shall make no law abridging, or, shall not be infringed. It's not that speech should generally not be abridged, or that gun rights are okay to infringe on just a little bit as long as hunting isn't impaired. Everyone has the right to a trial by jury of their peers, that doesn't just disappear if you've been bad.

Free speech and the right to bear arms are the first and second amendments because we need to be able to freely stand up to the government, and if, for whatever reason, the government doesn't listen we can make it. Even if Dorner was crazy, I haven't seen anything proving he wasn't, how would you act if the legal system was so corrupt that it protected murderers, rapists and sadists, then threw you out for reporting them. That, ladies and gentlemen, is why we have the second amendment and why it SHALL NOT BE INFRINGED.

Why Democrats are Anti Science

Yes the title was meant as Provocation. But in all seriousness neither dems nor reps are particularly good at the whole sciencing of things as demonstrated by the presidents speech last night. I say that because we heard about climate change and what we should do about it. This inevitably means subsidizing ineffective technologies while leaching tax money away from effective ones. In this case through the idea of a carbon tax.  All of this less than a week after the IPCC announced a 2 degree reduction in the estimates for future warming. 

Science is supposed to be data driven and falsifiable, the discussion around catastrophic climate change, particularly from the democrats, is decidedly not. Even though climate science has gotten incredible amounts of funding we hear more about children, polar bears and ad hominem attacks than we do about actual data. We hear more about new wind farms or green jobs than we do on the actual data surrounding their costs and net growth rates. It begs the question why.

The answer is that the data doesn't support the narrative.  The data says we lose at least 2 traditional jobs for every green job created. The data says we've lost billions to failed energy companies and that green jobs costs hundred of thousands or even millions of dollars per job. More importantly the data says that all of those green projects are an enormous waste of resources.  For all of the fanfare and end of the world speeches we heard regarding carbon dioxide and global warming, no one bothered to weed out  the natural variation, the bias or other effects. Well, except for the skeptics.

From Bjorn Lomberg's facebook page

Heres the abstract of the paper http://www.pnas.org/content/110/6/2058.abstract

See skeptics are slowly but surely chipping away at the numbers to determine how much of the warming was caused by CO2. That's kind of important, you see if it's assumed that CO2 is the principle driver of climate and all temperature increases are assumed to result from CO2 then predictions for warming are likely to be high. If that's not the case, and the warming is due to a variety of factors, then those predictions will be wrong.  Now when we chip away at the data sets, if CO2 is the main factor, then we should see relatively small reductions in the warming trends. 

What we have managed to extract so far is that actual decadal warming increases peaked out at between .12 and .16 degrees celsisus per decade. That's down from some analysis that indicated a possible .3 degree celsius decadal warming rate. In short the data says that actual warming is less than half what was being estimated. This didn't gain much positive press and was actually met with vitriol. Now more recent analysis cuts that trend in half again. Eliminating the data outlier of 1998 actually drops that rate a bit further. so in short our highest rate of warming which is based on the shortest window of data and includes a statistical outlier only comes to a maximum warming rate of .08 degrees celsius. we get that number just by cleaning up the noise in the data. We haven't even begun to deal with other thermal effects

The thing that doesn't get discussed a lot in the debate is that global warming as a theory has been around since about 1988. Until 2001 nobody cared, then Al Gore created a presentation, and while loaded with misrepresentations of data, and emotional pleas, terrified people. Skeptics have been trying to comb through the research and data ever since fighting an uphill battle against groups that are frankly better funded. We exist because there are some real questions about the methodologies, data and interpretation of the mainstream climate scientists. Even though climatologists had a 13 year head start, with papers and publications held in check only by their ambitions, better funding and the fact that it was their actual job the skeptics are making progress. We aren't winning because of a sudden funding increase, or greater acceptance. Were winning because the data disagrees with the narrative, and now, finally some scientists are taking notice. Democrats aren't.

At the end of the day it doesn't matter what the theory or the science says. If the data disagrees the science is shit end of discussion.

Ha Ha!! North Koreas Has Nukes

It's so funny it makes me cry, I mean really cry like sobbing.

http://www.bbc.co.uk/news/world-asia-21421841

For people who don't understand why Libertarians are against the wars in the middle east and excessive spending let me explain. There are real world threats, threats that can hit american cities and american citizens. We as a nation need to have the resources, the capital, the lending partners and political allies to deal with crises when they occur. We need to appear rational not vindictive, calm not aggressive, and by all means thoughtful not a mindless war machine.

We need to watch out for the Hitler's, the Stalin's and well anything that comes out of North Korea which is the definition of a crazy breeding ground. These are the people with armies, the professional kind not like the ones trained on a jungle gym. We need to look out for the people who would happily sit back and watch the world burn if they couldn't rule it, because those people are the actual threats. Those people and the ones who allow them to rule are crazy enough to give up their lives for a dark vision and false promises.

North Korea at Night: If you can get by the starvation

it's a great place for stargazing.

There are always going to be crazies who find a way to kill innocents, sometimes its a mass shooting, or a bombing or a plane crash. On 9/11 we lost over 3,000 american lives as a result of our actions since then we have lost over 6,000 more delivered by the government to the insurgents doors. Sure we allegedly got their leader, huzzah!! But what was the cost to our personal freedoms and liberties or...  the sheer dollar value.

"We are continuing this policy in bleeding America to the point of bankruptcy. Allah willing, and nothing is too great for Allah," Osama Bin Laden

Truth is if that was his goal he's winning. We pissed away money hunting and chasing an ideology. We burned political bridges and threatened civilians who were simply born in the country. We have spent the resources we need to stop a world war III on a dispute with a fringe group. Have we killed alot of insurgents or just general bad guys? sure, but the drone campaign is acting like a jihadist recruiting poster. It's like wielding a blade against a hydra every time we lop off a head two grow in its place.

We're a superpower and its time to start acting like one.  Lets put down our weapons in the middle east and try to let them deal with the problem. Even if al'qaeda remains they at least wont be able to easily target american soldiers and we wont be spending trillions of dollars to essentially recruit for them. We need to learn to live within our means and manage our responsibilities so when a real threat does emerge we don't turn to find our resources exhausted. We don't get paid to be the worlds police, it's time to stop acting like we do. 

Is there Climate change? a synopsis

So if you don't feel like reading the rather long previous posts let me summarize. First the research does support the theory of greenhouse gasses and the idea that man has had AN effect on our temperature. However the quantity of that effect as well as its significance is up for debate. Furthermore there is no actual evidence that proves causality or validates that any future warming will be catastrophic. While there are claims for catastrophic evidence none of them can prove causality and a great many of them have been invalidated with later research.

The truth is I got bored reiterating arguments I constantly make and didn't feel like delving into the issues surrounding the theory of climate forcing factors. I also didn't tackle the claims of extreme weather, or why it would be a psychologically popular theory. Quite frankly its pretty dull hearing that global warming/climate change/extreme weather will cause both more and less snow, warmer and colder winters increased drought and increased rain. Anyone even remotely knowledgeable on the subject knows that climate change is supposed to occur over long trends and that the data doesn't support the extreme weather hypothesis.

So what does that mean for us? ultimately we need to wait and see whats going to happen.  We need to recognize that there is always a shaman preaching how, if we just spend money in such a way, we can prevent bad things from happening.  Before throwing money in tax subsidies, breaks credits or mandatory purchasing agreements for the alternative energy crowd we should have proof that the investment will pay off, as it stands now we don't. Even if CO2 did raise the temperature to dangerous levels, it is still cheaper to build nuclear and natural gas power plants than wind and solar. They last substantially longer and in the case of natural gas we have already seen a reduction in atmospheric CO2.

Lets Have a Frank Discussion on Climate Change Part 4: The Skeptics Argument

The skeptics argument is first and foremost a criticism of the climate research itself. Now when I say criticism I'm not saying its a scolding or disagreement it means that there are questions concerning the methodology, results or assumptions used to determine those results.  Before a skeptic begins to offer their own analysis they need to explain what they find unsatisfactory about the existing research.  It can't simply be that they don't like it or its implications so lets start by examining the research on climate change in reverse order.

First most of the climate models have been found to be wildly inaccurate predicting recent temperature rises which have simply not occurred. Not that the temperature isn't rising, it is, just not as drastically as the models predicted. Nor is it anywhere near rapid enough to come close to the UN's IPCC worst case, or likely scenarios (please note this was the previous scenario not the recently released scenario which are still high compared to actual observation).  All the models predict a temperature that is much higher than actual observed warming. This indicates a non rational bias towards positive temperature forcing in both the models and literature supporting them.

Credit wattsupwiththat.com

As a matter of fact while the temperature has risen it is statistically insignificant meaning that it is indistinguishable from normal background variation. To be clear the period of temperature insignificance is half of the period of modern satellite records, which we have had for about 33 years. At this point you can almost claim that non warming is more the norm than warming. Strangely enough even with this observable data that technically falsifies the claims for CAGW there is an insistence that a mysterious cooling effect is in play and that warming will recommence, just wait and see I suppose. In some cases models are adjusted to try to back forecast observed temperature using various hypothesis as to what the mysterious force may be. It would seem that there is again a non rational bias or belief in warming that persists in the face of data.

The initial statements were to simply wait for the fifteen year mark before we get to call CAGW bullshit. After 16 years of no warming we now have to wait for 20 years to declare the models incorrect. While I appreciate the calls to patience, and understand that given the timescale of warming forces its important to wait,  ten years ago with only about 15 years of data warmists were calling for doom and gloom, emergency action the green economy and scrambling for Nobel prizes. To be clear 15 years of warming data are enough to call for action but 20 (or more) years are needed to call these theories bunk. It just seems biased.

Now even if we hit the 20 year mark and start to see statistically significant warming again shouldn't we wait another 40 years before declaring that warming is the norm? What if significant warming cycles are simply periodic oscillations? What if temperatures are to suddenly plummet? what happens to the models then? 

How far off are the models? well the least wrong is twice as high as actual climate. The SAR model predicted a temperature increase over the past decade of about .3 degrees and what we've actually seen is an increase of .12-.16 degrees. The IPCC estimated over the next century to be up to 6.4 degrees. Literally in order to hit this value wed need to see warming over the next 10 decades that is 4 times greater than a rate of warming we have ever seen.

That satellite record is important because while we do have temperature records dating back 150 years or so the farther back you go the less accurate they are. There are issues with quality control, widespread deployment and accuracy, as well as precision. Don't forget 30 years or so ago while computers did exist they were incredibly expensive and remote data collection methods were almost non existent and at best primitive. While we do have records that extend back 150 years, sampling errors and convenience bias are likely to create an impression of warming. But what about those records dating back hundreds or even thousands of years.

Those temperature records the ones that go back hundreds or even thousands of years have a large amount of scientific debate over them.  The oldest temperature records come from tree, ice and rock samples. They  are called proxy records as they approximate a temperature. There is ample arguments over their validity and they don't paint a perfect AGW or CAGW picture like say the hockey stick.

Michael Mann created this out of a set of data from tree rings and the subject matter is called dendrochronology. While there is ample scientific debate around the legitimacy of tree ring temperature proxies, the hockey stick graph once appearing in the IPCC's report on climate change has since been removed. The reason for this fall from grace was a simple statistical test, using a set of random junk data Mann's analysis algorithm produced a hockey stick. 

So in short it didn't matter whether he took actual results or not he still got a similar shape. In Mann's defense the peak was smaller but a smaller hockey stick is still a hockey stick and thus both pieces of evidence are irrelevant. Since then the data has been reevaluated and several algorithm's show no massive uptick in temperatures and histroical temperatures that may eve be higher. 

If you want to argue dendrochronology keep in mind that there is no means of recording or controlling the conditions which the trees grew in outside of the past few hundred years. As such tree ring data could proxy rainfall, sunlight, drought, CO2 and/or temperature.  Of course there was a recent article in nature which indicates the roman period may have been warmer than once believed, So take that as you like it

the ice cores that Al Gore used in his presentation were kind of a problem.

See how those two lines are seperated rather than overlapping? Well that's because the CO2 graph lagged the temperature graph by about 20 years.  So for years this has kind of been a problem for the pro warming community because it didn't support their theory. Granted it does make sense because of something called Raoul's law which deals with liquid gas saturation. The oceans hold CO2 and as they warm the gas is expelled colder oceans can hold more CO2. A warming period would have to start and warm the oceans before the gas is released thus validating the graph. The graphs were held apart to show the similarity between the curves without revealing the time function. This was literally disinformation.

That being said a recent study in nature found some way of having temperature lag CO2 if they start from the assumption that CO2 drives climate change and work backwards. Maybe Im exggerating but thats ind of how the abstract reads

"The co-variation of carbon dioxide (CO2) concentration and temperature in Antarctic ice-core records suggests a close link between CO2 and climate during the Pleistocene ice ages. The role and relative importance of CO2 in producing these climate changes remains unclear, however, in part because the ice-core deuterium record reflects local rather than
global temperature. Here we construct a record of global surface temperature from 80 proxy records and show that temperature is correlated with and generally lags CO2 during the last (that is, the most recent) deglaciation. "

Personally that is literally stating 'I believe this, haven't been able to prove it and here's how I'm gonna do it'.  That's not to say this is malicious, but it is seriously compromised objectivity. Attempting to explain the methodology, they didn't like the results from one inferred temperature record so they used other inferred temperature records to correct the previously inferred record. 

The geological proxy records are a bit more interesting from a skeptics point of view. not because they hold more weight or show some profound secret its because of what they don't show. See the geological proxy records show that we are not rising faster nor are we hotter than other warm periods. They also tend to be less stable and last for shorter periods of time than the extended ice ages in between. 

See that graph it shows the relatively short period of warming lasting about 11500 alongside the relatively long 100000 year glacial periods. We are well within natural variation 

That graph also shows CO2 and its pretty clear that there is a correlation. That being said fossil fuels have only been utilized for 150-250 years human beings have only been around for about 120,000 years so what was the climate driver 300,000 400,000 or 800,000 years ago.  If our fossil fuel emissions are whats driving climate now, then there would have to be some natural effect producing CO2 at the rate of a modern industrial society in a cyclic variation every hundred thousand years. Not only that but that the factor driving climate has to suddenly disappear at the end of the warming cycle. 

So lets have a synopsis of this information.
1. The models showing catastrophic warming don't agree with observed data.
2. The proxy records of historical warming don't find our current levels or rate to be outside of the historical norm.
3.  There seems to be a bias towards warming in data and results even to the point of some data being misrepresented.
4. There doesn't seem to be any major reason to assume catastrophic warming 6 degrees in 100 years
5. The IPCC estimates for temperature change range between 2-4x the rates ever observed.

Clearly the science behind the theory is solid, but there is no evidence that we are going to hit the levels required for catastrophic warming within the next century. The prediction models are wrong, and there doesn't seem to be enough data to suggest doing anything at the moment much less the drastic and expensive policies being pushed by warming proponents. This has led to a bevy of research into what I like to call warming catastrophe now tertiary studies. These studies will not be studying temperature related effects on a population they will be field studies that attempt to be causally linked to a warming planet. They always start with the conclusion the AGW can be observed through a trend and if no trend is observed they look for confounding variables.

There are lots of exaples of these such as this study in nature which found that phytoplankton, the oceanic food chain building block, was in decline. This would be devastating if true but thankfully a rebuttal was offered in nature. This rebuttal clearly illustrated the "observed" biomass loss was predominantly due to methodology not global warming. So there was an alternative explanation that accurately accounted for the observed phenomenon which was not considered pas AGW. Guess which publication was picked up and distributed by the Associated Press.

What about those poor polar bears? Al gore had them s the mascots of his presentation. suspended on ice that was disapearing.

No this isnt the inconveneint truth picture its awesomer (yes its a word)

The thing is polar bears don't spend their time living on ice flows they hunt on some sea ice after hibernation but then travel sometimes tens or even hundreds of miles to better feeding grounds.  In fact the whole arctic goes quiet in the winter months waiting for warmer waters that allow food to reproduce. but there was concern over polar bears and they became the mascots of the environmental movement against climate change. a study even found their population was on decline. But like I said a study as in one. because that study used a method called convenience sampling to only test the population of polar bears that was convenient to access from a human village where polar bears are considered a pest problem. Almost every other study has found the opposite. 

 The Inuit natives have been complaining about the polar bears increasing number. In fact the Hudson bay area where polar bear populations were thought to be on the decline was surveyed and found there were about 1000 bears doing just fine.  to be clear models predicted that the Hudson bay bear population should have dwindled to 650 individuals since 2004 but in fact there has been no change. No doubt that will also be blamed on climate change but there certainly isn't a mass polar bear extinction about to happen. 

What about our food supply, all those droughts and what not? Well yes we had a bad  drought but nowhere near as bad as the droughts in the 1950's or 1930's. IS it due to global warming? That's harder to answer. did it affect the food supply? a little bit but we still have more than enough to stuff our faces with whatever we want.  But that's not the only global warming may be affecting our food supply research with no actual evidence. 

There was this study in science which said that our food production has dwindled. this was based on a model predicting food production made in the 1980's and it ignored population growth. So while we are producing less food than anticipated our populations has grown by less than anticipated and our food growth has matched our population growth. Not to mention this assumes food production only from the top 5 grains and does not include the variety of foods which are now available due to increased household wealth and globalization. Does that mean the conclusion was wrong.... um yes? 

There are lots of other examples, pretty much anytime an association is made between warming and a population or trend there should be healthy skepticism. Not because its all false but because there is an inherent bias or assumption going into the study.  Correlation does not equal causation and the best example of this comes from the Flying Spaghetti Monsterism proof. 

Score One for the FSM

Before posting editing corrections understand this is a summary article and my opinion is tl;dr